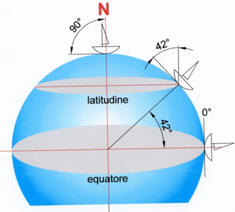
Altezza Solare e altezza Polare

Sappiamo tutti che la Terra compie una rotazione completa su se stessa in 24 ore e che in un anno compie una rivoluzione completa attorno al Sole. La rivoluzione terrestre si compie su di un piano che non è parallelo all’asse di rotazione ma si mantiene costantemente inclinato di 23,5°. Proprio questa inclinazione non permette al Sole di rimanere posizionato costantemente sulla verticale dello stesso parallelo ma muti la sua posizione quotidianamente avendo come limiti estremi il Tropico del Cancro e il Tropico del Capricorno che coincidono rispettivamente con le latitudini Boreale e Australe di 23,5°. Nella figura in cui si presuppone sia il Sole a compiere la rivoluzione attorno alla Terra si vede chiaramente che al solstizio estivo del 21 giugno, giorno più lungo dell’anno, i raggi solari colpiscono l’emisfero boreale alla massima latitudine consentita. Al solstizio invernale il 21 dicembre, giorno più breve dell’anno, sei mesi dopo, i raggi solari irradiano maggiormente l’emisfero australe mentre alle nostre latitudini i raggi arrivano alquanto obliqui. Nello schema si prefigura l’osservatore sul parallelo 42° e sono indicati gli angoli formati con l’orizzonte e rispettivamente da un lato con la Stella

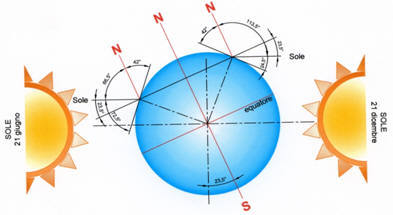
Polare e dall’altro con il Sole di mezzogiorno nelle due date solstiziali.  Naturalmente tra i due solstizi il Sole viene a trovarsi perpendicolare all’asse terrestre e pertanto sulla verticale della circonferenza equatoriale nella posizione equinoziale del 21 marzo e del 23 settembre che corrispondono all’uguaglianza tra il giorno e la notte. Traducendo graficamente quanto esposto nella successiva immagine possiamo osservare che la Stella Polare dista 42° dall’orizzonte del Nord, mentre all’opposto, all’orizzonte del Sud, il Sole si presenta lungo il meridiano corrispondente al mezzodì locale con i valori angolari che variano secondo il periodo dell’anno. Agli equinozi il Sole avrà una altezza corrispondente al complemento della latitudine:
 

Equinozi = 90° - 42° = 48°

Ai solstizi il Sole si distanzia alternativamente di 23,5° per cui avremo:

Solstizio Estivo = 48° +23,5° = 71,5°

Solstizio Invernale = 48° -23,5° = 24,5°
 

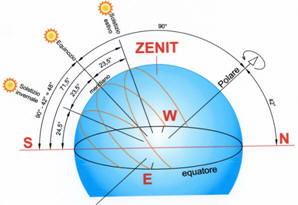
Nascendo quotidianamente sull’orizzonte Est il Sole aumenta progressivamente la sua altezza sino ad attraversare il meridiano per poi abbassarsi progressivamente verso Ovest fino a tramontare. Per determinare l’altezza del Sole al meridiano nelle due date equinoziali per una qualsiasi località è sufficiente sottrarre da 90° la latitudine del luogo. Per fare un semplice esempio trovandoci alla latitudine di Bolzano pari a 46° 29’, agli equinozi il meridiano sarà attraversato dal Sole ad una altezza sull’orizzonte di 90° - 46°29’ = 43°31’. Per determinare l’altezza solare meridiana per un’altra data dovremo sommare algebricamente all’altezza equinoziale il valore della declinazione solare usando le tavole calcolate. Dall’esempio sopra per il 10 maggio troviamo nella tavola un valore di declinazione decimale di +17,52 pari a 17°31’ ed avremo:
 

altezza solare meridiana = 43° 31’ + 17° 31’ = 61° 2’
 

Per la data invernale del 12 dicembre troviamo nella tavola un valore di declinazione decimale di -22,9992 pari a 22° 59’ ed avremo:
 

altezza solare meridiana = 43° 31’ - 22° 59’ = 20° 32’
 

Questi valori devono essere considerati approssimativi in quanto la tabella della declinazione solare riporta normalmente valori medi e non tiene conto della rifrazione dei raggi solari.

L’argomento riferito al moto apparente del Sole e tutte le sue implicazioni rispetto la gnomistica sarà ripreso più volte per approfondirne progressivamente l’argomento.

vedi esperimento