|
Radianti e
Trigonometria
Ci sono varie
misure angolari, cioč sistemi per misurare un angolo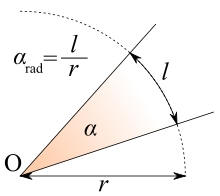 .
Il metodo che probabilmente vi č pių usuale č il sistema
sessagesimale, che si basa sulla divisione dell'angolo giro
in 360 "gradi angolari". Il numero 360 per
l'angolo giro
č scelto per motivi storici, ma dal punto di
vista matematico non é molto vantaggioso. Per molti scopi č molto
pių utile passare a un altro sistema, la misura in radianti.
Qui la grandezza di un angolo si misura come lunghezza dell'arco
corrispondente su una circonferenza di raggio 1. Ciō č
rappresentato nella figura qui a fianco: Invece di misurare l'angolo
a
in gradi, si usa la lunghezza dell'arco
l
come misura per la sua grandezza. L'angolo
giro in
radianti č
dato dalla circonferenza del cerchio di raggio 1, cioč da
2p. .
Il metodo che probabilmente vi č pių usuale č il sistema
sessagesimale, che si basa sulla divisione dell'angolo giro
in 360 "gradi angolari". Il numero 360 per
l'angolo giro
č scelto per motivi storici, ma dal punto di
vista matematico non é molto vantaggioso. Per molti scopi č molto
pių utile passare a un altro sistema, la misura in radianti.
Qui la grandezza di un angolo si misura come lunghezza dell'arco
corrispondente su una circonferenza di raggio 1. Ciō č
rappresentato nella figura qui a fianco: Invece di misurare l'angolo
a
in gradi, si usa la lunghezza dell'arco
l
come misura per la sua grandezza. L'angolo
giro in
radianti č
dato dalla circonferenza del cerchio di raggio 1, cioč da
2p.
|
Conversione da radianti a
angoli decimali |
Conversione da angoli
decimali a radianti |
|
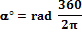 |
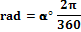 |
La
trigonometria č la parte della matematica che studia le funz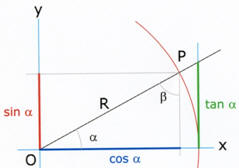 ioni
circolari. Data una circonferenza di raggio unitario con il centro
nell'origine e assumendo il senso antiorario come positivo, il punto
P mobile sulla circonferenza individua un arco e un angolo
corrispondente.
Il
seno
(sin) e il
coseno
(cos) dell'angolo θ sono due funzioni periodiche di periodo 2p
definite come l'ordinata e l'ascissa del punto P. La
tangente
(tan) č definita come il rapporto sin θ / cos θ, ed č una funzione
periodica di periodo p. Le altre funzioni trigonometriche sono la
secante (sec θ = 1/cos θ) la cosecante (cosec θ = 1/sin
θ) e la cotangente (cotan θ = 1/tan θ). ioni
circolari. Data una circonferenza di raggio unitario con il centro
nell'origine e assumendo il senso antiorario come positivo, il punto
P mobile sulla circonferenza individua un arco e un angolo
corrispondente.
Il
seno
(sin) e il
coseno
(cos) dell'angolo θ sono due funzioni periodiche di periodo 2p
definite come l'ordinata e l'ascissa del punto P. La
tangente
(tan) č definita come il rapporto sin θ / cos θ, ed č una funzione
periodica di periodo p. Le altre funzioni trigonometriche sono la
secante (sec θ = 1/cos θ) la cosecante (cosec θ = 1/sin
θ) e la cotangente (cotan θ = 1/tan θ).
La relazione
trigonometrica fondamentale č:
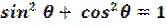
dalla quale
derivano le seguenti relazioni trigonometriche:
sinēθ = tanēθ/(1+tanēθ
) cosēθ = 1/(1+tanēθ) tanēθ = sinēθ/(1-sinēθ)
sinēθ = 1-cosē
θ cosēθ = 1-sinēθ tanēθ = (1-cosēθ)/cosē
θ
Valgono le seguenti relazioni:
sin (p/2
- α) = cos α (p/2
- α) = sin α
sin (p/2
- α) = cos α cos (p/2
- α) = sin α
sin (p
- α) = sin α cos (p
- α) = - cos α
sin (p
+ α) = - sin α cos (p
+ α) = - cos α
formule di
addizione:
sin (α+β) =
sin α cos β + sin β cos α
cos (α+ β) = cos α cos β - sin
α sin β
tan (α+ β) = tan α tan β / ( 1
- tan α tan β )
|
formule
di duplicazione: |
sin (2α) = 2
sin α cos α
cos (2α) =
cosē α - sinē α = 2 cosē α 1
tan (2α) =
tanē α / ( 1 - tanē α ) |
|
formule
di prostaferesi: |
sin α + sin
β = 2 sin [(α+β)/2] cos [(α-β)/2
sin α - sin
β = 2 sin [(α-β)/2] cos [(α+β)/2
cos α + cos
β = 2 cos [(α+β)/2] cos [(α-β)/2
cos α - cos
β = -2 sin [(α+β)/2] sin [(α-β)/2 |
|
formule
di bisezione: |
sinē (α/2) =
(1 - cos α)/2
cosē (α/2) =
(1 + cos α)/2 |
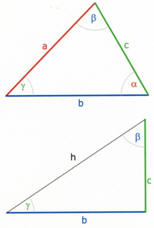 Relazioni
tra lati e angoli di un triangolo Relazioni
tra lati e angoli di un triangolo
Dato un triangolo qualunque di lati a,b,c e angoli opposti
corrispondenti α, β,γ valgono le seguenti formule:
teorema dei seni:
a / sin α
= b / sin β = c / sin γ
teorema di Carnot:
aē = bē +
cē - 2 b c cos α
Dato un triangolo
rettangolo valgono le seguenti relazioni:
b = h sin β
b = h cos γ
b = c tan β |
 .
Il metodo che probabilmente vi č pių usuale č il sistema
sessagesimale, che si basa sulla divisione dell'angolo giro
in 360 "gradi angolari". Il numero 360 per
l'
.
Il metodo che probabilmente vi č pių usuale č il sistema
sessagesimale, che si basa sulla divisione dell'angolo giro
in 360 "gradi angolari". Il numero 360 per
l'
