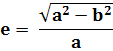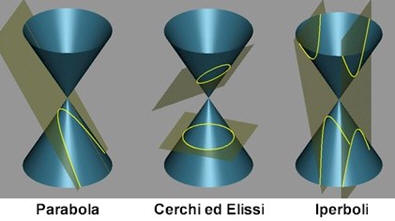
Le Coniche

Il cono è una figura solida originata dalla rotazione di una retta obliqua rispetto l’asse di rotazione. Il sezionamento del cono mediante piani con angolazioni differenti da origine a figure piane chiamate coniche che appartengono a specifiche famiglie di curve di secondo grado che si caratterizzano  da un parametro chiamato eccentricità. Le citate figure comprendono le elissi,  la parabola, le iperboli ed il cerchio che ne rappresenta un caso particolare. L’eccentricità della curva, denominata con la lettera e, varia da 0 per il cerchio, minore di 1 per le elissi, pari a 1 per la parabola e maggiore di 1 per le iperboli. Il cerchio si ottiene sezionando il cono con un piano perpendicolare all’asse del cono mentre inclinando il piano, si ottengono le elissi con eccentricità crescente. Quando il piano di sezione raggiunge l’inclinazione pari al profilo del cono l’elisse, si chiude e diventa una parabola. Le iperboli si ottengono con inclinazioni del piano sezionante maggiori. Queste particolari curve sono molto importanti in astronomia per descrivere le orbite dei corpi celesti e inoltre vengono spesso utilizzate nella gnomica.

Ellisse – Si tratta di una figura piana consistente in una curva chiusa e simmetrica rispetto i propri assi maggiore e minore. Oltre al centro della figura sull’asse maggiore si posizionano due punti, equidistanti dal centro, denominati fuochi dell’elisse. Una caratteristica dell’elisse consiste nell’avere tutti i punti a una distanza dai due fuochi tale che la loro somma è costante e pari all’asse maggiore. Indicato con a il semiasse maggiore, con O il centro, con F1 e F2 i due fuochi, ne segue che:

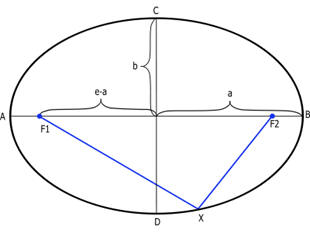
2a = F1 - p + F2 - p

La distanza dal centro di un fuoco si indica con c e vale: c = a e
 

dove e rappresenta l’eccentricità e da una misura dell’allungamento dell’ellisse. L’ellisse ha un’eccentricità, come detto, variabile tra 0 e 1 sebbene quest’ultimo valore non possa essere tecnicamente raggiunto. Con eccentricità 0 l’ellisse diviene un cerchio e i due fuochi sono coincidenti con il centro, aumentando l’eccentricità l’ellisse si allunga sempre più finché con eccentricità 1 si chiude solo all’infinito, in questo caso cessa di essere un’ellisse e diviene una parabola.

dove a e b rappresentano il semiasse maggiore e minore. Nelle coordinate polari il raggio variabile r (lettera greca rho) dell’elisse, chiamato raggio vettore, è funzione dell’angolo n (lettera greca ni), compreso fra l’asse maggiore e il raggio vettore con verticale in uno dei due fuochi

dove p rappresenta una quantità caratteristica dell’elisse esprimibile come:

oppure  dove k è la distanza tra la direttrice e il fuoco

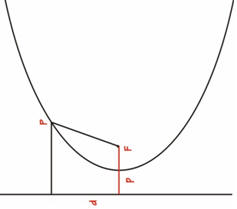
Parabola – La parabola ha eccentricità pari a 1 ed è costituita da una curva che si chiude solo all’infinito. La definizione geometrica la descrive come l’insieme dei punti equidistanti da una retta d, denominata direttrice, e da un punto fuoco F. Assunta p la distanza tra il fuoco e la direttrice si evince che il punto parabolico più vicino alla direttrice dista p/2 sia dalla direttrice che dal fuoco.

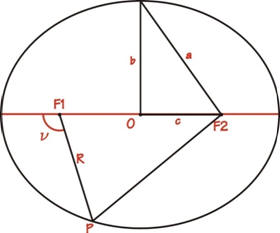
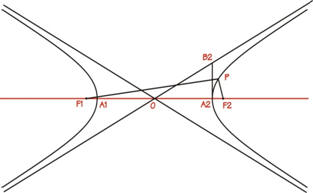
Iperbole - Le iperboli sono delle curve aperte che hanno una eccentricità maggiore di 1 e sono costituite da due curve formate da due serie di punti che hanno differenza costante fra le distanze da due punti chiamati fuochi F1 e F2.

valore assoluto ( P-F1 - P-F2 ) = 2a

dove 2a è la distanza fra le curve sull’asse contenente i fuochi (a = O-A1 e a = O-A2), si definisce inoltre 2c la distanza tra i due fuochi e O il punto intermedio (c = O-F1 e c = O-F2). I rami dell’iperbole tendono asintoticamente a due rette, queste formano un triangolo rettangolo con l’asse dei fuochi tale che in corrispondenza del cateto O-A2 (o OA1) si trova il cateto A2-B2 che vale b.