|
Elevazione e
sustilare
La direzione dello
gnomone
rispetto il
quadrante dell’orologio, co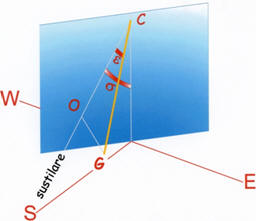 munque
orientato, è determinata dall’elevazione
e dall’angolo sustilare
che a loro volta dipendono dalla
latitudine
nonché dall’inclinazione
e dalla declinazione
del quadrante.
L’elevazione
e l’angolo sustilare
sono le indicazioni più dirette e utili
per installare uno
gnomone
perfettamente orientato con l’asse
terrestre elevandolo dell’angolo
Ô
dalla
sustilare perpendicolarmente al
quadrante.
Un pratico esempio è costituito dallo
gnomone
triangolare o a vela in cui l’ipotenusa è lo
gnomone
polare,
un cateto è l’ortostilo
e l’atro cateto è collocato sulla linea
sustilare
in modo tale gli estremi coincidano l’uno con il centro del munque
orientato, è determinata dall’elevazione
e dall’angolo sustilare
che a loro volta dipendono dalla
latitudine
nonché dall’inclinazione
e dalla declinazione
del quadrante.
L’elevazione
e l’angolo sustilare
sono le indicazioni più dirette e utili
per installare uno
gnomone
perfettamente orientato con l’asse
terrestre elevandolo dell’angolo
Ô
dalla
sustilare perpendicolarmente al
quadrante.
Un pratico esempio è costituito dallo
gnomone
triangolare o a vela in cui l’ipotenusa è lo
gnomone
polare,
un cateto è l’ortostilo
e l’atro cateto è collocato sulla linea
sustilare
in modo tale gli estremi coincidano l’uno con il centro del
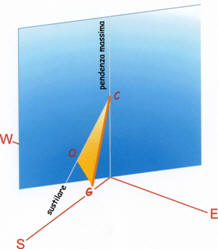 quadrante
e l’altro con il piede. Il triangolo è un piano perpendicolare al
quadrante
e l’elevazione
è l’angolo avente come vertice il centro del
quadrante.
Anche per calcolare le altre linee e curve che normalmente appaiono
sui quadranti solari l’elevazione
e l’angolo sustilare
costituiscono un riferimento
essenziale. La formula per calcolare l’elevazione
può fornire risultati sia positivi che negativi indicando che lo
gnomone
dovrà puntare rispettivamente verso l’alto e verso il basso. I
quadranti
orizzontali hanno
elevazione
positiva mentre i
verticali diretti
hanno
elevazione negativa, gli
equinoziali
hanno 90° di
elevazione,
positiva il
superiore e negativa quello
inferiore,
i quadranti
polari hanno una
elevazione
nulla per definizione. quadrante
e l’altro con il piede. Il triangolo è un piano perpendicolare al
quadrante
e l’elevazione
è l’angolo avente come vertice il centro del
quadrante.
Anche per calcolare le altre linee e curve che normalmente appaiono
sui quadranti solari l’elevazione
e l’angolo sustilare
costituiscono un riferimento
essenziale. La formula per calcolare l’elevazione
può fornire risultati sia positivi che negativi indicando che lo
gnomone
dovrà puntare rispettivamente verso l’alto e verso il basso. I
quadranti
orizzontali hanno
elevazione
positiva mentre i
verticali diretti
hanno
elevazione negativa, gli
equinoziali
hanno 90° di
elevazione,
positiva il
superiore e negativa quello
inferiore,
i quadranti
polari hanno una
elevazione
nulla per definizione.
Formula dell’elevazione
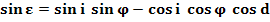
La formula dell’angolo
sustilare restituisce sempre valori
positivi che esplicitamente no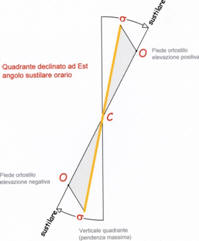 n indicano se la
sustilare
si trova ruotata in modo orario o antiorario rispetto alla
verticale. Buona regola è considerare, con
declinazioni
di quadrante
a Est, la retta
sustilare
ruotata in senso orario e di considerare la semiretta inferiore
rispetto al centro del
quadrante C
per
le elevazioni negative. n indicano se la
sustilare
si trova ruotata in modo orario o antiorario rispetto alla
verticale. Buona regola è considerare, con
declinazioni
di quadrante
a Est, la retta
sustilare
ruotata in senso orario e di considerare la semiretta inferiore
rispetto al centro del
quadrante C
per
le elevazioni negative.
Angolo sustilare
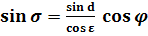
Quando l’elevazione
è nulla lo
gnomone è contenuto nel
quadrante
che in questo caso si chiama
quadrante polare.
Questi
quadranti possono essere identificati
con i piani che ruotano attorno allo
gnomone
che ne costituisce l’asse. Per ottenere la formula per calcolare la
declinazione
data l’inclinazione
si pone l’elevazione
a 0° e si risolve la formula per l’elevazione
rispetto alla
declinazione.
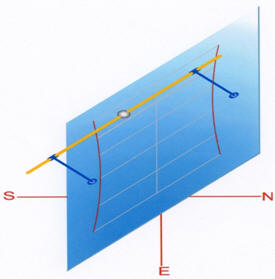
Quadranti polari

con inclinazione
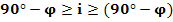
Nella formula trovata si evince anche che, in
valore assoluto, l’inclinazione
non può essere maggiore della
colatitudine.
Uno gnomone
contenuto nel piano di un
quadrante,
come negli
orologi polari, non è idoneo a
proiettare alcuna ombra. A questo aspetto si ovvia installando un
segmento di
gnomone polare traslandolo dal
quadrante
parallelamente a se stesso. Il
punto stella
può essere un punto qualsiasi dello
gnomone
oppure un nodo appositamente inserito.
Le formule
dell’elevazione e dell’angolo
sustilare,
per declinazioni e inclinazioni particolari, si possono risolvere
ottenendo le formule semplificate per i quadranti principali.
|
Formula elevazione e angolo sustilare per i principali
quadranti |
|
quadrante |
i |
d |
elevazione |
ora sustilare |
|
VERTICALE DIRETTO |
i = 0° |
d = 0° |
e
= -(90° -
j) |
s = 0° |
|
VERTICALE DECLINATO |
i = 0° |
d = … |
sin
e
-cos
j
cos d |
sin
s
= sin d/cos
e)
cos
j |
|
ORIZZONTALE |
i = 90° |
d = 0° |
e = j |
s = 0° |
|
EQUINOZIALE SUPERIORE |
i =
j |
d = 180° |
e
= 90° |
s = 0° |
|
EQUINOZIALE INFERIORE |
i = -j |
d = 0° |
e
= -90° |
s = 0° |
|
POLARE |
i = 0° |
d = 90° |
e
= 0° |
s = 90° - j |
|
POLARE INCLINATO |
cos d = tan i tan
j |
e = 0° |
sin
s
= sin d cos
j |
|
90° -j
>= i >= -(90° -j) |
|
 munque
orientato, è determinata dall’
munque
orientato, è determinata dall’ quadrante
quadrante n indicano se la
n indicano se la
