|
Curve Diurne
Agli
equinozi
l’orbita apparente
del
Sole si trova in un piano ed ha
cen
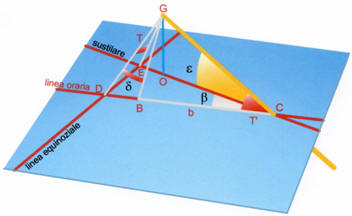
Le declinazioni del Sole possono pertanto essere evidenziate sul quadrante tracciando le coniche, ellisse, parabola o iperbole, che tagliano le linee orarie nel punto B in modo tale che le lunghezze d’ombra b risultino pari al segmento BC.
L’eccentricità della
conica dipende dalla
declinazione del
Sole, dalla
latitudine e naturalmente
dall’orienta-mento del
quadrante.
Normalmente si trovano i punti B
di i
Calcolo angolo fra lo gnomone e linea oraria
Vediamo ora la formula per calcolare la distanza b presumendo riferirsi ad una linea oraria per la quale è stato già calcolato l’angolo b e dipendente inoltre dalla lunghezza gnomonica I e dalla declinazione solare d identificante la curva diurna che si intende tracciare.
Distanza centro
Quadrante e oraria e una curva diurna
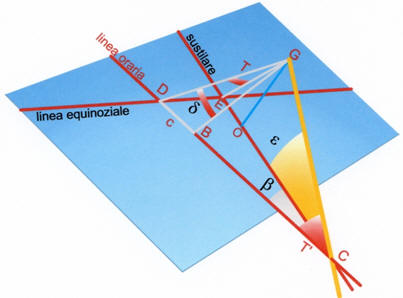
Angolo b massimo
Angolo orario T massimo
Quando si presentano
angoli orari
di valore superiore a Tmax
la lunghezza dell’ombra b
diviene negativa e pertanto non proiettabile sul
quadrante.
Con determinate
declinazioni la
linea oraria
può avere b
negative ed essere invece positiva con altre comportando che a
quella determinata ora il Sole proietterà ombre sul
quadrante
solo in un determinato periodo dell’anno. Va precisato con chiarezza
che in una data
declinazione l’angolo
orario massimo è di fatto un limite
geometrico dell’orologio stante che l’illuminazione ponga limiti
restrittivi o viceversa. Il limite all’angolo
orario
derivante dall’illuminazione mette in evidenza l’impossibilità dello
gnomone
a proiettare ombre con il Sole sotto l’orizzonte mentre il
limite imposto da
b
max
è
geometrico stante che evidenzia l’impossibilità del Sole a
proiettare ombre sul
quadrante
oltre un certo
angolo orario
data l’elevazione
stilare e una
data
declinazione
del Sole. Bisogno tenere inoltre conto che l’angolo
orario Tmax
è
simmetrico rispetto all’ora
sustilare
mentre il
semiarco diurno è simmetrico rispetto
al mezzogiorno
vero locale
e pertanto questi due intervalli possono in generale limitarsi
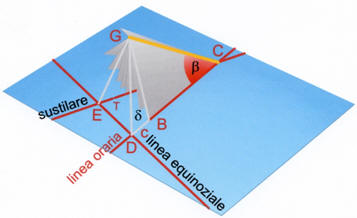
Semiarco diurno
Nei casi di declinazioni nulle Tmax e a risultano entrambi di 90° corrispondenti a 6 ore che in un orologio verticale declinato a Ovest, a partire dall’ora sustilare precedente il mezzogiorno, impediscono all’ombra di segnare il tramonto, mentre invece all’alba il quadrante consentirebbe di segnare ombre con orari addirittura precedenti l’illuminazione.
La formula calcolante C si semplifica notevolmente negli orologi polari essendo in questi il centro del quadrante C all’infinito mentre l’elevazione Ô è nulla. 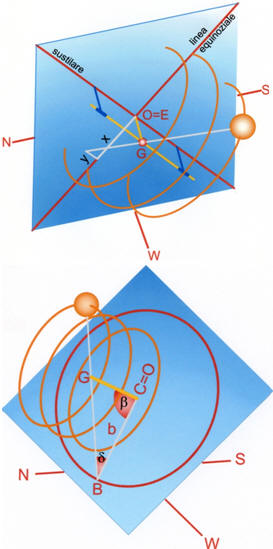
Distanza su una
linea orariatra le
Stante che in questi orologi tutte le linee orarie sono parallele alla sustilare risulta possibile utilizzare un sistema cartesiano che abbia quali ascisse l’equinoziale e come ordinata la sustilare. La curva diurna sarà quindi calcolata nei suoi punti con propria equazione ed in modo scollegato dalle linee orarie.
Coordinate
cartesiane delle curve
Gli orologi equinoziali, per qualsiasi angolo orario T, hanno un angolo b sempre di 90° facendosi che si semplifichi la formula per calcolare b e che l’ortostilo g coincida con lo gnomone I.
Distanza dal centro
del quadrante dell’intersezione tra
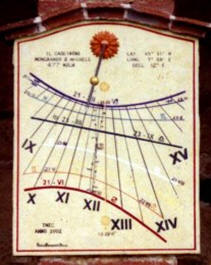
Rimane invece inutilizzabile la formula calcolante C dato che l’equinoziale risulta essere un circolo di raggio infinito che rende conseguentemente la distanza C anch’essa infinita a prescindere da qualunque angolo orario T e declinazione del Sole d. La curva diurna risulta essere un circolo di raggio b e a qualsiasi declinazione la lunghezza d’ombra b sarà sempre uguale e indipendente dalla linea oraria. Il Sole raggiunge ogni sua declinazione d due volte l’anno in due differenti giorni. Questo ripetersi cronologico della declinazione solare allunga l’ombra da un solstizio all’altro per tornare ad accorciarsi nel ciclo annuale. Due volte l’anno l’ombra gnomonica avrà la stessa lunghezza corrispondente alla stessa declinazione solare e coinciderà per due date diverse con ogni curva diurna del quadrante. Nei quadranti si tracciano normalmente le curve diurne corrispondenti e rappresentanti le declinazioni solari delimitanti i periodi zodiacali che separano due segni in aumento di declinazione e altri due segni in fase di diminuzione di declinazione. Per rappresentare curve diurne rappresentanti i dodici segni dello Zodiaco dovremmo quindi tracciare sette curve diurne delle quali una è l’equinoziale.
|
 tro nel
tro nel 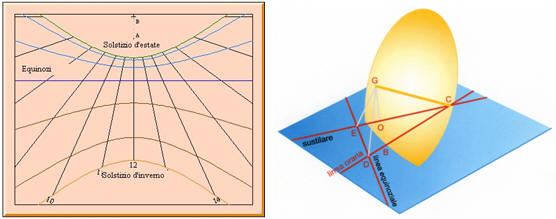
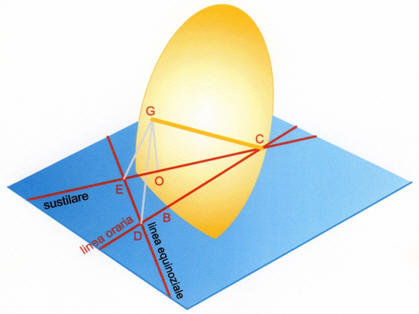
 ntersezione con le
ntersezione con le