|
Orizzonte del
Quadrante
Quando il
Sole si defila all’orizzonte il
quadrante non
può essere r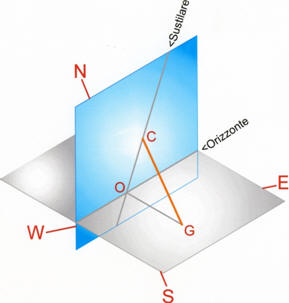 aggiunto
dai raggi di luce. Conseguentemente al fatto che le
orbite apparenti
si adagiano su una sfera che ha per centro il
punto stella,
l’orizzonte
del
quadrante di
un
orologio solare
consiste in una retta che si genera dall’intersezione di un piano
orizzontale che toccando il
punto stella
taglia sempre orizzontalmente il piano
quadrante.
Con il Sole sopra l’orizzonte, la luce solare, passando per
il
punto stella,
tocca il
quadrante
sotto la retta dell’orizzonte.
Questo significa che le porzioni di
linee orarie
e
curve diurne
eventualmente poste al di sopra della
linea dell’orizzonte
non possono mai essere raggiunte dall’ombra. La linea dell’orizzonte
può essere tracciata sul
quadrante
calcolando sulla
sustilare la
distanza denominata o
tra il piede dell’ortostilo
e l’intersezione con la
linea orizzontale.
Nei casi in cui si intenda installare un ortostilo o
gnomone
incompleto o
può essere calcolato tramite l’ortostilo
g
(vedi
OG). aggiunto
dai raggi di luce. Conseguentemente al fatto che le
orbite apparenti
si adagiano su una sfera che ha per centro il
punto stella,
l’orizzonte
del
quadrante di
un
orologio solare
consiste in una retta che si genera dall’intersezione di un piano
orizzontale che toccando il
punto stella
taglia sempre orizzontalmente il piano
quadrante.
Con il Sole sopra l’orizzonte, la luce solare, passando per
il
punto stella,
tocca il
quadrante
sotto la retta dell’orizzonte.
Questo significa che le porzioni di
linee orarie
e
curve diurne
eventualmente poste al di sopra della
linea dell’orizzonte
non possono mai essere raggiunte dall’ombra. La linea dell’orizzonte
può essere tracciata sul
quadrante
calcolando sulla
sustilare la
distanza denominata o
tra il piede dell’ortostilo
e l’intersezione con la
linea orizzontale.
Nei casi in cui si intenda installare un ortostilo o
gnomone
incompleto o
può essere calcolato tramite l’ortostilo
g
(vedi
OG).
Distanza
dell’orizzonte dal piede dell’ortostilo sulla sustilare
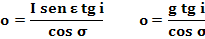
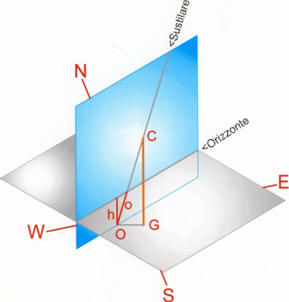 Le distanze
possono essere calcolate, anziché sulla
sustilare,
sulla verticale del
quadrante che
passa per il piede dell’ortostilo.
Con la lettera h
viene
definita la distanza dell’orizzonte
dal piede dell’ortostilo
sulla sua verticale. Come per o
anche h
si può esprimere in funzione dell’ortostilo
g. Le distanze
possono essere calcolate, anziché sulla
sustilare,
sulla verticale del
quadrante che
passa per il piede dell’ortostilo.
Con la lettera h
viene
definita la distanza dell’orizzonte
dal piede dell’ortostilo
sulla sua verticale. Come per o
anche h
si può esprimere in funzione dell’ortostilo
g.
Distanza
dell’orizzonte dal piede dell’ortostilo sulla verticale
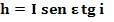
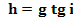
Nei casi in
cui la retta della linea dell’orizzonte viene a trovarsi al
di sotto del piede dell’ortostilo le formule danno risultati
di segno negativo.
|
Formula distanza dell’orizzonte dal piede
ortostilo su sustilare |
|
quadrante |
i |
d |
o |
h |
|
VERTICALE DIRETTO |
i = 0° |
d = 0° |
0 |
0 |
|
VERTICALE DECLINATO |
i = 0° |
d = … |
0 |
0 |
|
ORIZZONTALE |
i = 90° |
d = 0° |
infinito |
infinito |
|
EQUINOZIALE SUPERIORE |
i =
j |
d = 180° |
I tg
w
= g tg
w |
I tg
w
= g tg
w |
|
EQUINOZIALE INFERIORE |
i = -j |
d = 0° |
-I tg
w
= -g tg
w |
-I tg
w
= -g tg |
|
POLARE |
i = 0° |
d = 90° |
0 |
0 |
|
POLARE INCLINATO |
cos d = tg i tg
j |
g tg i / cos
s |
g tg i |
|
90° -j
>= i >= -(90° -j) |
|
Per i
quadranti
principali queste si possono semplificate e in particolare negli
orologi verticali,
comunque questi siano
declinati, l’orizzonte
passa per il piede dell’ortostilo
mentre nei
quadranti orizzontali
il piano del
quadrante è
parallelo al piano dell’orizzonte,
non genera rette di intersezione, riceve l’illuminazione del Sole
in modo illimitato. Le formule si riferiscono alle distanze dal
piede dell’ortostilo
ma è inoltre anche possibile considerare queste distanze dal centro
del
quadrante
quale misura oC
sulla
sustilare.
La distanza sulla verticale tra il piede dell’ortostilo
e il centro del quadrante viene indicata col le lettere
hC.
|
Distanza del
centro del quadrante
dall’ortostilo sulla sustilare
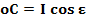 |
Distanza del
centro del quadrante
dall’ortostilo sulla verticale
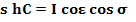 |
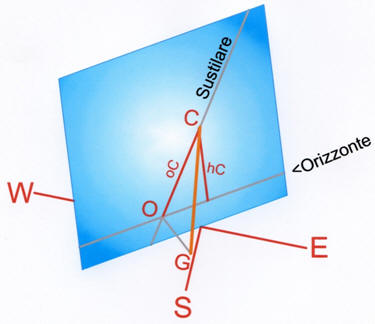 Anche se il
quadrante
non è illuminato, la linea dell’orizzonte
può fornire utili indicazioni. Considerando l’intersezione di una
curva diurna
con la linea dell’orizzonte
si può, quando non così fortunati che in quel punto transiti proprio
una
linea oraria,
immaginare valutando a quale orario corrisponda e questo sarà, per
le date corrispondenti alla
curva diurna,
l’orario dell’alba
o del
tramonto.
All’alba
e al
tramonto
l’illuminazione del
quadrante
può essere impedita dal suo orientamento e in questo caso le
curve diurne
non sono intersecate dalla linea dell’orizzonte.
La valutazione fatta potrà comunque essere confermata dalla formula
del
semiarco diurno
a
che è funzione della
declinazione
e quindi porterà allo stesso risultato corrispondente all’angolo
orario
tra il mezzogiorno e l’alba
o il
tramonto. Anche se il
quadrante
non è illuminato, la linea dell’orizzonte
può fornire utili indicazioni. Considerando l’intersezione di una
curva diurna
con la linea dell’orizzonte
si può, quando non così fortunati che in quel punto transiti proprio
una
linea oraria,
immaginare valutando a quale orario corrisponda e questo sarà, per
le date corrispondenti alla
curva diurna,
l’orario dell’alba
o del
tramonto.
All’alba
e al
tramonto
l’illuminazione del
quadrante
può essere impedita dal suo orientamento e in questo caso le
curve diurne
non sono intersecate dalla linea dell’orizzonte.
La valutazione fatta potrà comunque essere confermata dalla formula
del
semiarco diurno
a
che è funzione della
declinazione
e quindi porterà allo stesso risultato corrispondente all’angolo
orario
tra il mezzogiorno e l’alba
o il
tramonto.
|
 aggiunto
dai raggi di luce. Conseguentemente al fatto che le
aggiunto
dai raggi di luce. Conseguentemente al fatto che le  Le distanze
possono essere calcolate, anziché sulla
Le distanze
possono essere calcolate, anziché sulla  Anche se il
Anche se il